Центростремительное ускорение в природе не существует.
Это очередная ошибка в физике, которую необходимо исправить.
Откуда появилась формула центростремительного ускорения ![]() ?
?
В энциклопедиях написано, что первым к этому приложил руку Гюйгенс. Пускай будет Гюйгенс.
Давайте, разберёмся прав он или нет?
Наука физика – это представления человека о природе. Человек старается смоделировать и описать процессы, происходящие в природе. Для описания процессов и однозначного их толкования ввели термины и их обоснования.
Вот основные термины, применяемые в механике:
— работа-энергия, обозначение ![]() .
.
Этих терминов достаточно для описания моделей процессов в механике. Ничего другого не должно быть.
1. Сначала рассмотрим процесс равномерного и прямолинейного движения тела или частицы в пространстве.
Тело или частица, движущееся прямолинейно и равномерно в пространстве, обладает мощностью
2. Теперь рассмотрим процесс равномерного движения тела или частицы по окружности.
Какие могут быть варианты такого процесса? Например, вариант с грузом, подвешенным на верёвке, или вариант обращения планеты вокруг звезды.
Как рассуждал Гюйгенс, выводя формулу для центростремительного ускорения?
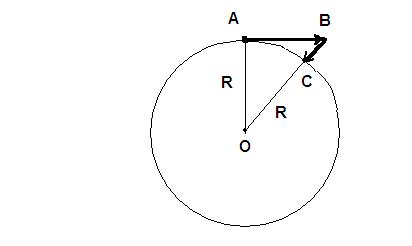
Тело движется равномерно по окружности с радиусом ![]() и со скоростью
и со скоростью ![]() . В данный момент времени тело находится в точке
. В данный момент времени тело находится в точке ![]() и имеет скорость
и имеет скорость ![]() .
.
Это изображено на рис. 1.
Рис. 1
Тело хочет двигаться прямолинейно по инерции, но центростремительная сила возвращает его на линию окружности.
Гюйгенс предлагает, пусть путь ![]() будет движением вперёд, а отрезок
будет движением вперёд, а отрезок ![]() будет возвратом тела на линию окружности. Тогда из треугольника
будет возвратом тела на линию окружности. Тогда из треугольника ![]() по закону Пифагора
по закону Пифагора
Подставим эти обозначения в теорему Пифагора
Так как время ![]() очень маленькое, то последним членом можно пренебречь. Тогда после преобразования этого выражения получится
очень маленькое, то последним членом можно пренебречь. Тогда после преобразования этого выражения получится
![]() — центростремительное ускорение.
— центростремительное ускорение.
Этот процесс Гюйгенс смоделировал и описал неправильно, ошибочно.
В чём ошибки Гюйгенса?
Первая ошибка. На участке ![]() движения тела Гюйгенс применяет в качестве характеристики перемещения скорость
движения тела Гюйгенс применяет в качестве характеристики перемещения скорость ![]() , а на участке
, а на участке ![]() ни с того, ни с сего вдруг применяет ускорение
ни с того, ни с сего вдруг применяет ускорение ![]() . Оснований делать это никаких. Это просто несерьёзно.
. Оснований делать это никаких. Это просто несерьёзно.
А как должно быть на самом деле?
На участке ![]() скорость надо представить как линейную
скорость надо представить как линейную ![]() , а на участке
, а на участке ![]() как центростремительную скорость
как центростремительную скорость ![]() , которая является результатом гравитационного взаимодействия. Никаких ускорений нет. Все перемещения характеризуются скоростями перемещения. В рассмотренном процессе две скорости
, которая является результатом гравитационного взаимодействия. Никаких ускорений нет. Все перемещения характеризуются скоростями перемещения. В рассмотренном процессе две скорости ![]() ,
,![]() и их результирующая скорость
и их результирующая скорость ![]() . Или даже точнее, Вы сами вектор скорости реального движения
. Или даже точнее, Вы сами вектор скорости реального движения ![]() раскладываете на составляющие
раскладываете на составляющие ![]() и
и ![]() .
.
Вторая ошибка. Далее. Линейную скорость ![]() и радиус окружности
и радиус окружности![]() Гюйгенс посчитал известными измеряемыми величинами. Однако это не так. Линейная скорость
Гюйгенс посчитал известными измеряемыми величинами. Однако это не так. Линейная скорость ![]() (или
(или ![]() ), вектор которой является касательной к окружности, это воображаемая скорость, то есть замерить её невозможно. А, что мы тогда измеряем? Мы измеряем реальную скорость
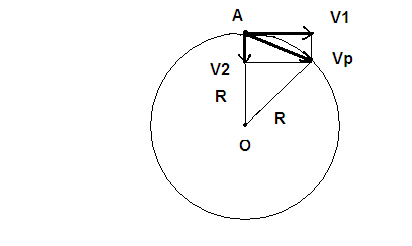
), вектор которой является касательной к окружности, это воображаемая скорость, то есть замерить её невозможно. А, что мы тогда измеряем? Мы измеряем реальную скорость ![]() , связанную с конкретным перемещением тела в пространстве. Это изображено на рис. 2. Вот те на, а “современная” физика и астрономия об этом не знают, или не хотят знать, или запрещено знать, и думают, что измерили линейную скорость.
, связанную с конкретным перемещением тела в пространстве. Это изображено на рис. 2. Вот те на, а “современная” физика и астрономия об этом не знают, или не хотят знать, или запрещено знать, и думают, что измерили линейную скорость.
Третья ошибка. Рисунок модели процесса, представленный Гюйгенсом, ошибочен, он не соответствует действительности.
На рис. 2 по-новому размещены векторы скоростей данного процесса.
Вот заблуждение Гюйгенса. Он утверждает, что тело хочет двигаться прямолинейно по инерции, но центростремительная сила возвращает его на линию окружности. Однако это не так. Правильно будет, тело хочет двигаться прямолинейно по инерции, но одновременно на тело действует ещё гравитационное взаимодействие, результатом которого является движение по окружности. Никакого возврата нет, тело всё время движется, имея результирующий вектор ![]() .
.
![]() — реальная скорость, которая измеряется согласно перемещению тела. Вектор реальной скорости всегда направлен к линии окружности и всегда касается линии окружности.
— реальная скорость, которая измеряется согласно перемещению тела. Вектор реальной скорости всегда направлен к линии окружности и всегда касается линии окружности.
![]() — линейная скорость, вектор которой является касательной к окружности.
— линейная скорость, вектор которой является касательной к окружности.
![]() — центростремительная скорость, вектор которой направлен к центру окружности.
— центростремительная скорость, вектор которой направлен к центру окружности.
Получается, что известны только реальная скорость ![]() и радиус окружности
и радиус окружности ![]() . Неизвестны линейная скорость
. Неизвестны линейная скорость ![]() и центростремительная скорость
и центростремительная скорость ![]() . Их необходимо рассчитать через известные
. Их необходимо рассчитать через известные ![]() и
и ![]() . Для этого в предложенной новой модели и её описании необходимо найти зависимость
. Для этого в предложенной новой модели и её описании необходимо найти зависимость ![]() и
и ![]() от
от ![]() и
и ![]() . Эта зависимость носит более сложный характер, чем формула Гюйгенса. Но ведь придумывать формулы нельзя. Это получается не моделирование, не описание, а нечто другое.
. Эта зависимость носит более сложный характер, чем формула Гюйгенса. Но ведь придумывать формулы нельзя. Это получается не моделирование, не описание, а нечто другое.
Рис. 2
Теперь необходимо найти зависимость ![]() и
и ![]() от
от ![]() и
и ![]() .
.
Рассчитаем линейную скорость ![]() и центростремительную скорость
и центростремительную скорость ![]() через измеряемые параметры движения тела по окружности
через измеряемые параметры движения тела по окружности ![]() реальную скорость и радиус окружности
реальную скорость и радиус окружности ![]() .
.
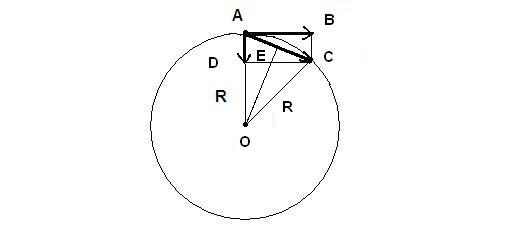
Рис. 3.
Зададимся временем процесса, равным единице измерения времени ![]() . На рис. 3 из точки
. На рис. 3 из точки ![]() проведём перпендикуляр к отрезку
проведём перпендикуляр к отрезку ![]() до пересечения в точке
до пересечения в точке ![]() . Отрезок
. Отрезок ![]() представим, как путь
представим, как путь ![]() , тогда отрезок
, тогда отрезок ![]() , а отрезок
, а отрезок ![]() . Угол
. Угол ![]() равен углу
равен углу ![]() . Из треугольников
. Из треугольников ![]() и
и![]()
Решая эту систему уравнений, получим
Имейте в виду, что![]() не является ускорением, а формула
не является ускорением, а формула ![]() вовсе не описывает ускорение. Если
вовсе не описывает ускорение. Если ![]() , то никакого изменения скорости нет и нет, соответственно, и ускорения. Правильная и полная формула изменения скорости (ускорения)
, то никакого изменения скорости нет и нет, соответственно, и ускорения. Правильная и полная формула изменения скорости (ускорения) ![]() ,
,
В нашем случае ![]() и поэтому не означает, что это ускорение. Наличие
и поэтому не означает, что это ускорение. Наличие ![]() это следствие того, что отрезок пути равный не выражен через скорость и время.
это следствие того, что отрезок пути равный не выражен через скорость и время.
Скорость тела за единицу времени равную будет
Мы рассмотрели рассуждения Гюйгенса и исправили допущенные им ошибки. Теперь надо более подробно рассмотреть процесс равномерного движения тела по окружности с рассмотрением мощностных характеристик, участвующих в данном процессе. Всегда необходимо начинать рассмотрение и разбор процессов с мощности. Это та характеристика, которой обладает тело или частица.
Рассмотрим два варианта.
Первый вариант. Груз, привязанный к верёвке. Человек рукой передаёт мощность движения грузу
Верёвка не даёт грузу улететь по касательной. Эта мощность направлена к центру окружности. Её назвали центростремительной. Вот мощность, которую она развивает
![]() — центростремительная скорость.
— центростремительная скорость.
Реальная мощность движущего по окружности груза складывается из суммы мощностей ![]() и
и ![]() по принципу суперпозиции
по принципу суперпозиции
Реальная скорость движения груза по окружности ![]() складывается из суммы скоростей
складывается из суммы скоростей ![]() и
и ![]() по принципу суперпозиции
по принципу суперпозиции
Второй вариант. Система Солнце и Земля. Будем считать, что Земля движется вокруг Солнца по окружности. Эксцентриситет у Земли самый маленький из всех планетных тел, кроме спутников Юпитера. Там они вовсе ничтожные.
Итак, Земля обладает мощностью инерции
Земля старается за счёт инерции двигаться прямолинейно, но гравитационное взаимодействие (эфирные частицы), действующие с внешних сторон, заставляют Землю и Солнце двигаться вокруг общего центра масс.
Как это эфир выполняет?
Коротко про эфир здесь
http://zhurnal.lib.ru/editors/n/nikolaew_s_a/dokladnamezhdunarodnomkongresse-2010.shtml
Более подробно про эфир здесь
http://zhurnal.lib.ru/n/nikolaew_s_a/ewoljucionnyjkrugoworotmateriiwowselennoj5izdanie2009g.shtml
Эфирные частицы передают свою суммарную мощность (сейчас это называют кинетическая энергия ![]() ) с внешних сторон Земле и Солнцу. Вектор этой суммарной мощности направлен к общему центру масс.
) с внешних сторон Земле и Солнцу. Вектор этой суммарной мощности направлен к общему центру масс.
Суммарная мощность эфирных частиц, передаётся массе Земли, в результате чего Земля приобретает центростремительную скорость
где ![]() — суммарная масса эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии,
— суммарная масса эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии,
![]() — скорость эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии,
— скорость эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии,
![]() — центростремительная скорость.
— центростремительная скорость.
Мощность и скорость реального движения определяются по принципу суперпозиции (принципу векторного сложения мощностей и скоростей), заметьте скоростей, а не ускорений.
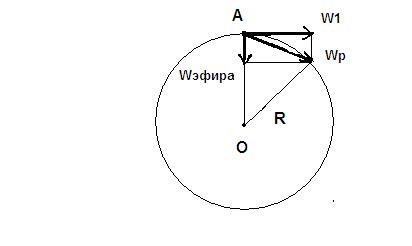
На рис. 4 показана схема векторов мощностей действующих на Землю. Земля находится в точке А, Солнце находится в точке О.
Рис. 4.
Таким образом, мы измеряем реальную скорость движения планеты, связанную с перемещением, а линейная скорость неизвестна, она воображаемая. Не думайте, что Вы измерили линейную скорость. Линейную скорость ещё необходимо рассчитать. Также необходим расчет, если нужно, и центростремительной скорости (рис. 2).
где ![]() — вектор реальной скорости перемещения планеты по окружности,
— вектор реальной скорости перемещения планеты по окружности,
![]() — вектор центростремительной скорости.
— вектор центростремительной скорости.
Процесс движения тел по окружности необходимо рассматривать, именно, таким образом, исходя из терминов, которые мы договорились использовать в механике. Если быть честным и принципиальным, то в физике всё (как в макро, так и в микромире) объясняется на основе механики и этих терминов, которые мы договорились использовать.
Вот статья об этом
http://zhurnal.lib.ru/n/nikolaew_s_a/kwantowachmehanikalandau.shtml
Выводы.
1. В описываемом процессе движения тела по окружности, есть линейная, центростремительная и результирующая этих скоростей, а ускорений никаких нет и, в частности, центростремительного.
2. Линейная скорость также как и центростремительная скорость, расчётные величины. Измеряется только реальная скорость, которая является результирующей от этих скоростей.
3. Формула центростремительного ускорения ![]() ошибочная и к тому же не точная, так как при её выводе пренебрегли одним слагаемым.
ошибочная и к тому же не точная, так как при её выводе пренебрегли одним слагаемым.
А теперь посмотрим, что означает ”пренебрежём последним членом слагаемого“, который отличается от предыдущего члена степенью в квадрате?
Какова ошибка от такого пренебрежения?
Проверим. Возьмём любое число меньше единицы, например, 0,1.
В квадрате это число станет 0,01.
Теперь у нас два числа, по формуле с сокращением последнего члена, и без его сокращения.
Одно без сокращения 0,1 + 0,01 = 0,11.
Другое с сокращение 0,1.
Эти два числа отличаются друг от друга на 10%.
Если взять число 0,2, то погрешность составит 12%.
Если взять число 0,9, то погрешность составит 19%.
Таким образом, ошибка вычислений по ”красивой“ формуле Гюйгенса ![]() находится во втором знаке и составляет от 10% до 19%, в зависимости от величины первой цифры, а эта цифра может быть любой.
находится во втором знаке и составляет от 10% до 19%, в зависимости от величины первой цифры, а эта цифра может быть любой.
Ошибка, вычисленная по формуле Гюйгенса, даже не является методической (закономерной).
Можно ли такой формулой пользоваться?
И чем в таком случае занимается ”современная“ физика?
А, вот чем. Сидят инженеры или астрономы или другие ”учёные“ и вычисляют центростремительное ускорение с точностью кто до 5, а кто до 7 знака и более.
Как это назвать?
Подходит только одно слово – идиотизм.
4. Схема, предложенная Гюйгенсом для моделирования, для описания и расчёта характеристик этого процесса (рис. 1), ошибочная.
5. Отсутствует причина порождающая центростремительную силу.
6. Раз не существует центростремительного ускорения, то нет и центростремительной силы. Кроме того, сила по формуле Гюйгенса ![]() — это изменение количества движения. Какое может быть изменение количества движения у тела, движущегося равномерно по окружности, ведь масса тела не изменяется и скорость тоже
— это изменение количества движения. Какое может быть изменение количества движения у тела, движущегося равномерно по окружности, ведь масса тела не изменяется и скорость тоже ![]() ,
, ![]() .
.
7. Гравитационное взаимодействие характеризуется не силой, а мощностью, которую переносит и передаёт эфир. Переноситься и передаваться может только мощность объектов (тел или частиц). Сила переноситься и передаваться не может. Сила – это ошибочные представления Гюйгенса в механике. Мнения Гюйгенса и Ньютона по многим вопросам физики фундаментально расходились. В основном труде Ньютона ”Математические начала натуральной философии“ понятие термина сила (на латыни DINAMYS) играет совсем другую роль, чем в механике Гюйгенса. Перевод законов Ньютона с латыни Эйлер произвёл просто неправильно, некорректно. Об этом в следующих статьях.
* * *
Кто-нибудь использовал ошибочное название центростремительного ускорения для серьёзных доказательств в физике?
Да, конечно! Им был Ландау.
В природе всё взаимосвязано и правильно. Например. Электрон, обращаясь по стационарной орбите вокруг ядра атома, не излучает – это первый постулат Н.Бора. Значит орбита круговая, а движение равномерное, без ускорений. Всё логично, электрон движется равномерно без ускорения по орбите, которая круговая, поэтому не излучает.
А некоторые “учёные” в “современной” физике хотят всё это запутать.
Вот отрывок из статьи.
“………В ”современной“ физике подвергается сомнению тот факт, что известная классическая физика (механика с электродинамикой) может быть использована для исследования микромира.
В качестве путеводителя выбран сборник трудов Л.Д.Ландау и Е.М.Лившица.
Почему именно Л.Д.Ландау и Е.М.Лившиц? Другие иногда скрывают сомнительные места своих трудов, ухитряясь облекать заведомую чепуху в форму легенд, да так, чтоб читатель проморгал подмену. А эти авторы откровенны, так как заведомо были уверены в дремучести читателя – вроде время тогда в нашей стране поощряло дремучесть, а сообразительность карало всё больше расстрелом.
В самом начале учебника Л.Д.Ландау, Е.М.Лившица ”Квантовая механика“, ГИ, физ.-мат.лит., Москва, 1963 г. на странице 13 читаем:
”……Классическая механика и электродинамика при попытке применить их к объяснению атомных явлений приводят к результатам, находящимся в резком противоречии с опытом. Наиболее ясно это видно уже на противоречии получающегося при применении обычной электродинамики к модели атома, в которой электроны движутся вокруг ядра по классическим орбитам. При таком движении как при всяком ускоренном движении зарядов, электроны должны были бы непрерывно излучать электромагнитные волны. Излучая, электроны теряли бы свою энергию, что должно было бы привести в конце концов к падению на ядро.
Таким образом, согласно классической электродинамике, атом был бы неустойчив, что ни в какой степени не соответствует действительности…..“.
Что я могу сказать про это.
Либо Ландау очень дремучий в физике, либо задание дурачить лохов.
Во-первых. Что, Ландау не знаком с постулатами Н.Бора или не согласен с ними?
Во втором постулате Н.Бора ясно сказано, что электроны, двигаясь по своим орбитам, не излучают, а излучают только при переходе с одной орбиты на другую.
Из постулата следует, что электрон, двигаясь по орбите, не имеет ускорения. Орбита круговая. Это всем ясно, кроме Ландау.
Во-вторых. Утверждать, что когда заряд движется, то он излучает – это неверно, это просто невежество. В качестве примера-доказательства. Электрон в электронно-лучевой трубке. Электрическое поле разгоняет электрон. Электрон движется ускоренно от катода к аноду и не излучает. А излучает только лишь при торможении. Торможение – это смена знака ускорения. Все в электротехнике это знают, кроме Ландау. Тоже происходит при переменном токе. Электрическое поле, пока растёт напряжение, разгоняет электроны, а при спаде напряжения формируется квант и излучается. И так везде в электротехнике.
В-третьих. Где Ландау увидел изменение скорости электрона при его движении по орбите вокруг ядра атома? Линейная и угловая скорости у электрона постоянные. Меняется только направление движения и всё. А это не ускорение. Центростремительное ускорение неудачное название параметра в этом процессе. Поменяйте название. В физике таких вещей много. Всё равно когда-то придётся поменять и навести во всех терминах порядок. Везде нужна логика.
Но Ландау хватается всего лишь за неудачное название, надеясь на дремучесть аудитории. Ведь может кто-то не знает, что такое ускорение и его формулу
И вообще, как можно подобное выдавать за серьёзную научную аргументацию?
Своё неуменье объяснить некоторые процессы природы Ландау спешит представить как неспособность классической механики и электродинамики.
Оказывается виновата классическая механика и электродинамика.
Вот Вам и основа для квантовой механики.
Как мы выяснили, оказывается, оснований для похорон классической механики и электродинамики нет. Есть только некомпетентность Ландау в вопросе обращения электрона вокруг ядра атома.
Ну, а что же такое квантовая механика?………….“.
Продолжение про Ландау здесь
http://zhurnal.lib.ru/n/nikolaew_s_a/kwantowachmehanikalandau.shtml
Используемые источники:
1. Николаев С.А. “Эволюционный круговорот материи во Вселенной”. 6-ое издание,
СПб,2010 г., 320 с.
2. Николаев С.А. ”Ошибочный перевод Эйлера законов Ньютона“. СПб,2011 г., 44 с.



 Март 22nd, 2012
Март 22nd, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике 
Hello there! This article could not be written any better! Looking at this article reminds me of my previous roommate! He continually kept talking about this. I most certainly will forward this article to him. Pretty sure he’ll have a good read. Thanks for sharing!
Видео ролики онлайн…
Подробнее читайте на сайте…