Физика — параноидное фэнтези, ФАКТЫ.

Из истории механики

Семен А. Николаев

Россия, Санкт-Петербург

Март 12, 2013

Аннотация

В данной работе исследуются обоснованность и подлинность модели механики, которой мы пользуемся в настоящее время.

В конце 17 века было два учёных, у каждого из которых, как пишут в старых энциклопедиях, была своя механика. И эти механики были фундаментально противоположны друг другу. Этими учёными были Гюйгенс (1629 – 1695 г.) и Ньютон (1643 – 1727 г.).

У Ньютона не было новой модели механики, он продолжал дело Галилео Галилея (1564 – 1642 г.) и Рене Декарта (1596 – 1650 г.).

А Гюйгенс придумал новую модель механики.

Итак, две модели механики.

Одна модель механики основана на передаче инерции  от одних тел или частиц другим телам или частицам в виде соударений. Для передачи взаимодействий на расстояние, эта модель механики предусматривала в качестве переносчика взаимодействий наличие определённой модели эфира (эту модель эфира ещё в 1690 году предложил Фатио, но её запретили к печати, об этом в конце статьи). Как видно, причина взаимодействия тел, частиц или зарядов в этой модели механики обязательно связана с соударениями тел или частиц между собой, или передачи инерции от эфирных частиц телам или зарядам, также в виде соударений. Материальным переносчиком взаимодействий на расстоянии являются эфирные частицы. Основателем такой модели механики считается Г. Галилей (1564 – 1642 г.). Поддержал его Декарт (1596 – 1650 г.) и Ньютон (1643 – 1727 г.).

Другая модель механики, в отличие от предыдущей модели, основана на ”некой“ силе . В качестве объяснения передачи взаимодействия на расстоянии через пустоту между телами, частицами или зарядами применяется ”некая“ сила. В данной модели механики отсутствует материальный переносчик взаимодействий. Другими словами отсутствует причина взаимодействий. Модель такой механики обходится без наличия эфира. Такую модель механики придумал Гюйгенс (1629 – 1695 г.). Поддержал его Лейбниц (1646 – 1716 г.), дав ей название ”живая“ сила.

Вернёмся в те времена и рассмотрим, как всё это было. (Тогда ещё никто не подозревал о существовании единичного взаимодействия, сейчас Вы называете это гравитационная постоянная).

Греки Аристарх Самосский (310 — 230 г. до н.э.) и Гиппарх из Никеи (190 — 120 г. до н.э.) определили размер Луны и расстояние до неё. Они сравнивали при затмении размеры тени Земли и Луны с их реальными размерами. Расстояние до Луны вышло 384.395 км, а Луна получалась в 4 раза меньше Земли.

Иоганн Кеплер (1571 – 1630 г.), используя материалы астрономических измерений Тихо Браге (1546 – 1601 г.), начертил орбиты планет. Исследуя движение планет по этим орбитам, Кеплер выявляет в 1609 г. три закономерности. С помощью этих закономерностей Кеплер определил относительные расстояния и схему Солнечной системы. Но её масштабы оставались пока не разгаданными, кроме расстояния до Луны. Много позже на помощь пришло простейшее изобретение – параллакс. Тогда повторно определили расстояние до Луны, а затем до планет и Солнца.

Нам понадобится третья закономерность Кеплера  для орбит всех планет.

Ньютон, проанализировав схему Солнечной системы, заметил ещё одну закономерность. Инерция, удерживающая планеты на орбитах, прямо пропорциональна произведению массы центрального тела (Солнца) на массу планеты и обратно пропорциональна расстоянию между ними.

Для системы Солнце — планеты:  и ,

где  – инерция, удерживающая планеты на орбите,

 — масса планеты,

 — масса Солнца.

 — центростремительная скорость планеты или начальная скорость свободного падения, направленная к Солнцу.

Для системы Земля – Луна: , 

где  — масса Луны,

— масса Земли.

Примечание. Во времена Гюйгенса и Ньютона гравитационная постоянная ещё не была определена. Поэтому везде будет стоять знак пропорциональности (). В те времена ещё было пропорциональное исчисление. Например, плотность Земли в 5,48 раз больше плотности воды. Или, масса Луны в 81 раз меньше массы Земли. В те времена никому и в голову не приходило, что может быть как-то по-другому. Пропорциональное исчисление продолжается до сих пор, но немного в другом качестве. Например, взята определённая масса, и она объявлена эталоном и все остальные массы сравниваются с массой эталона. По принципу, если веса сравниваемых масс равны, то равны и их массы. То же самое и с измерением длины, температуры и т. д. Везде пропорциональное сравнение, разница лишь в том, если можно экспериментально вычислить, то приоритет за ним.

Ситуация, в которой закон Ньютона был без гравитационной постоянной, продолжалась долго. Только в 19 веке (но это был эксперимент не Кавендиша 1799 г.) экспериментально определили величину единичного взаимодействия (гравитационную постоянную) . Тем самым, подтвердив экспериментально так называемый закон всемирного тяготения Ньютона. Имейте ввиду, что перевод Эйлера совершенно не означает подлинность смысла слов в законах Ньютона и даже сам переводимый текст.

В дальнейшем Ньютон распространил найденную им закономерность на всю механику, возведя её в ранг фундаментального закона .

Однако Ньютон предупреждал, что этот закон для дальних расстояний, то есть массы представлены точками. На близких расстояниях необходимо учитывать размеры взаимодействующих тел, иначе будет ошибка. Но это тема отдельного разговора.

Гюйгенс тоже проанализировал третью закономерность Кеплера. И вот что он заметил. Если равенство  для всех планет преобразовать, вставив  и , то получим ту же закономерность, но записанную в другом виде:  то же для всех планет.

Что это за постоянное число ? Не трудно было догадаться, что это число характеризует массу центрального тела (характеризует, но не равно, примечание автора). Например, Солнце в системе Солнце – планеты или Землю в системе Земля – Луна.

Вот как это выглядело:  и .

Далее Гюйгенс берёт две формулы Ньютона.

Одна формула инерции, с которой Луна хочет упасть на Землю , где  — начальная скорость падения.

Другая формула гравитационного взаимодействия между Луной и Землёй .

Гюйгенс приравнивает их между собой .

Затем вместо массы Земли вставляет найденное им выражение .

Вот что получается: .

После произведённых сокращений остаётся 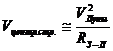. Однако с формулой Ньютона не совпадает размерность. Гюйгенсу почему-то не догадаться, что центростремительная скорость это и есть начальная скорость свободного падения. Просто для одной скорости много разных названий. Поэтому Гюйгенсу надо было центростремительную скорость заменить ускорением свободного падения. Но чтобы пользоваться формулой Ньютона для инерции надо обратно использовать начальную скорость свободного падения.

Что делает Гюйгенс в этой ситуации? Вместо ускорения свободного падения он применяет центростремительное ускорение . Затем это выражение возвращает в формулу Ньютона . К этой формуле Вы давно привыкли. Она только без гравитационной постоянной, которую вычислят и введут в формулу только в 19 веке.

Далее вот что произошло. Центростремительное ускорение для Луны, вычисленное по формуле Гюйгенса, совпало с ускорением свободного падения Луны на Землю, вычисленное через ускорение свободного падения на поверхности Земли и расстояния до Луны.

Центростремитель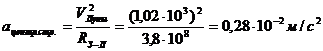ное ускорение .

Ускорение свободного падения .

Ускорение свободного падения на поверхности Земли, экспериментально измеренное . Расстояние до Луны в 60 раз больше радиуса Земли. Ускорение свободного падения уменьшается с высотой в квадратичной зависимости.

Как видно  и  почти совпали.

Гюйгенс сделал вывод, что центростремительное ускорение равно ускорению свободного падения. Гюйгенс посчитал, что ускорение свободного падения, это как бы частный случай центростремительного. На основании этого Гюйгенс хочет распространить эту формулу  на всю механику и сделать фундаментальным законом.

Давайте сразу проверим, подходит ли эта формула, кроме движения планет по устойчивым орбитам, ко всему остальному, например, к поверхности Земли. То есть другими словами, совпадёт ли ускорение свободного падения на поверхности Земли с центростремительным ускорением точек поверхности Земли.

Ускорение свободного падения на поверхности Земли .

Скорость точек поверхности Земли .

Центростремитель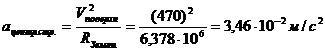ное ускорение .

Как видите,  не совпадает с . Это доказывает, что формула применима только для движения планет по устойчивым орбитам, и называть её следует ускорением свободного падения. Но и это всё равно связано только одним всего на всего совпадением. Поэтому масса Солнца, рассчитанная через ускорение свободного падения  тоже под вопросом, и естественно массы всех планет Солнечной системы?

Перед Гюйгенсом встаёт задача, чтобы распространить эту формулу на всю механику, а не только астрономию, нужно как-то её ”вывести“.

А теперь посмотрим, что придумал Гюйгенс, чтобы ”вывести“ эту формулу для всех тел, движущихся по окружности.

Как рассуждал Гюйгенс, ”выводя“ формулу для центростремительного ускорения?

Рассуждения Гюйгенса взяты из энциклопедии.

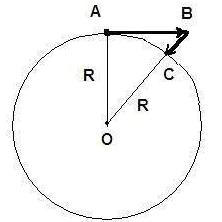
Тело движется равномерно по окружности с радиусом  и со скоростью . В данный момент времени тело находится в точке  и имеет скорость . Это изображено на рис. 4.

Тело хочет двигаться прямолинейно по инерции, но центростремительная сила возвращает её на линию окружности. Гюйгенс предлагает, пусть путь  будет движением вперёд, а отрезок будет возвратом тела на линию окружности. Тогда из треугольника  по закону Пифагора,

,,.

Подставим эти обозначения в теорему Пифагора.

 Рис. 4.

.

Так как время  очень маленькое, то последним членом можно пренебречь. Тогда после преобразования этого выражения получится ,

где  — линейная скорость тела,

 — центростремительное ускорение.

Этот процесс Гюйгенс смоделировал и описал неправильно, ошибочно.

В чём ошибки Гюйгенса?

Первая ошибка. На участке  движения тела Гюйгенс применяет в качестве характеристики перемещения скорость . А на участке  вдруг применяет ускорение . Оснований это делать нет. Это просто несерьёзно.

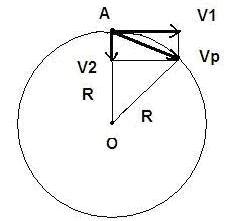
А как должно быть на самом деле? Это изображено на рис. 5.

 — реальная скорость, которая измеряется согласно перемещению тела, вектор реальной скорости всегда направлен к линии окружности и всегда касается линии окружности.

 — линейная скорость, вектор которой является касательной к окружности.

 — центростремительная скорость, вектор которой направлен к центру окружности.

Если тело движется по окружности, то скорости ,  и  обязательно связаны между собой соотношением .

Рис 5.

На участке  скорость надо представить как линейную , а на участке  как центростремительную скорость . Никаких ускорений нет. Все перемещения характеризуются скоростями перемещения. В рассмотренном процессе две скорости ,  и их результирующая скорость . Или даже точнее, Вы сами вектор скорости реального движения  раскладываете на составляющие  и .

Вторая ошибка. Далее. Линейную скорость  и радиус окружности  Гюйгенс посчитал известными измеряемыми величинами. Однако это не так. Линейная скорость  (или ), вектор которой является касательной к окружности, это воображаемая скорость, то есть замерить её невозможно. А, что мы тогда измеряем? Мы измеряем реальную скорость , связанную с конкретным перемещением тела в пространстве. Это изображено на рис 5. Например. Если по окружности движется тело, то реальная скорость  перемещения тела по окружности будет . Если рассматриваем движение планеты, тогда то же самое. Вчера планета была в точке А, а сегодня находится уже в точке С. Астрономы расстояние АС делят на время и получают скорость перемещения .

Третья ошибка. Рисунок модели процесса, представленный Гюйгенсом, ошибочен, он не соответствует действительности. На рис. 5 по-новому размещены векторы скоростей данного процесса. Вот заблуждение Гюйгенса. Он утверждает, что тело хочет двигаться прямолинейно по инерции, но центростремительная сила возвращает его на линию окружности. Однако это не так.

Дело в том, что случаев движения тел по окружности много.

Рассмотрим некоторые основные и дадим заключение: может ли тело сначала улетать за линию окружности, как нарисовано у Гюйгенса, а потом возвращаться?

Первый случай. Если движение тела не связано с гравитацией, то чтобы тело двигалось по окружности, оно должно быть обязательно жёстко связано с центром вращения (тело на верёвке, тело на жёсткой спице или сплошное тело). Телу хочется лететь по инерции по касательной со скоростью , но верёвка или спица будут ограничивать траекторию движения тела линией окружности, создавая центростремительную скорость , направленную к центру. Совершенно очевидно, что тело не может в данном случае улетать за линию окружности, а затем возвращаться. Всё происходит одновременно, и никакого возврата нет, тело всё время движется по окружности, имея результирующий вектор . Никакой центростремительной силы не существует. Если верёвка порвётся, то тело полетит по касательной с линейной скоростью , которую можно замерить. Связи с радиусом эти скорости не имеют. Рисунок, рассуждения и формула Гюйгенса, которой пользовались, ошибочна.

Второй случай. Движение незакреплённых тел в центрифуге. Можете повторить известный эксперимент, заснятый на плёнку, а потом просматриваемый на замедленной скорости. Расположите шарики на дне горизонтальной центрифуги на разном расстоянии от центра. Произведите съёмку при включении центрифуги. В момент начала вращения центрифуги, все шарики двигались по касательной. Достигнув стенки барабана центрифуги, они стали вращаться вместе с центрифугой как единое целое. Если мысленно убрать стенку центрифуги, то шарики снова стали бы улетать по касательной.

Попробуйте для первого и второго случаев применить схему Гюйгенса (рис.4) для объяснения центростремительного ускорения. Например, шарики улетают из барабана центрифуги по касательной, согласно рис. 4 Гюйгенса. Потом центростремительная сила возвращает их на линию окружности. Как шарики могут через стенку барабана улететь, а затем вернуться назад снова через стенку барабана центрифуги?

Вывод. Таким образом, ни центростремительных, ни центробежных сил не существует. Существует центростремительная скорость, которая рассчитывается в разных случаях по-разному.

Третий случай. Движение звёзд вокруг центра масс галактики. В Солнечной системе все планеты движутся вокруг Солнца согласно законам Кеплера. Это случай, когда почти вся масса системы расположена в центре. В звёздных системах (в галактиках) звёзды и их массы распределены по всему объёму галактики. Как показывают наблюдения, звёзды в галактике не могут двигаться по законам Кеплера, как в Солнечной системе. Иначе спирали были бы все закручены на большое количество оборотов и наблюдаемого узора в виде спирали мы не наблюдали бы. Звёзды в галактиках обращаются не по законам Кеплера, а, вероятно, по закону близкому к движению сплошного тела.

Четвёртый случай. Движение планет вокруг Солнца под действием гравитационного взаимодействия. Земля и Солнце связаны между собой гравитационным взаимодействием. Инерцию для удержания Земли на орбите вокруг Солнца непрерывно создаёт эфир. Это мы называем притяжением. На самом деле эфирные частицы приталкивают Землю и Солнце друг к другу с внешних сторон, передавая им свою суммарную инерцию. Эти две суммарные инерции равны и направлены встречно друг к другу

 или

Суммарная инерция эфирных частиц, передаваемая Земле с массой , сообщает ей центростремительную скорость  (при каком-то определённом )

,

где  — суммарная масса эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии с внешней стороны Земли,

 — скорость эфирных частиц (нейтриников), участвующих в гравитационном взаимодействии с внешней стороны Земли,  — масса Земли,

 — центростремительная скорость Земли или начальная скорость свободного падения Земли на Солнце (начальная скорость свободного падения численно равна ускорению свободного падении ).

У нас имеется ещё одна формула гравитационного взаимодействия, в которой взаимодействие связано с расстоянием. Это формула Ньютона.

Заменим в формуле Ньютона  силу  на инерцию , а ускорение свободного падения на начальную скорость свободного падения . Получим две формулы, инерции в которых равны.

Инерции  и  равны,

где — единичная инерция, возникающая при взаимодействии масс равных по 1 кг каждая и расстоянии 1 м между ними, численно эта инерция равна гравитационной постоянной , а размерность её будет ;

 — начальная скорость свободного падения Земли на Солнце (начальная скорость падения численно равна ускорению свободного падения).

Приравняем инерцию, передаваемую эфирными частицами с внешней стороны Земли, но записанную разными формулами

 или .

Из всего рассмотренного надо сделать общий вывод.

1. В астрономии формула  обозначает ускорение свободного падения (и то под вопросом, так как основана только на одном случае совпадения на орбите Луны).

2. Центростремительного ускорения в природе не существует. В механике есть только центростремительная скорость.

3. Раз центростремительного ускорения не существует, то не существует и центростремительной силы.

4. Модель механики, основанная на силе, ошибочна.

5. Чтобы воспользоваться моделью механики Ньютона, основанной на инерции, надо силу заменить инерцией, а ускорение начальной скоростью движения.

 

ПРИМЕЧАНИЕ. Оказывается, гравитация была описана ещё во времена Ньютона. В 1690 году швейцарский математик Николас Фатио из Женевы предложил теорию эфира, которая объясняла гравитационное взаимодействие, описанное Ньютоном

,

где  — инерция, передаваемая эфирными частицами каждому телу, с внешних сторон,

 и  — массы тел,

 — расстояние между телами.

Объяснение было очень простым и материалистичным. Эфирные частицы летят во всех направлениях Вселенной и передают свою инерцию телам, приталкивая тела, друг к другу. Не вызывает сомнений, что описанное Фатио словами, совпадает с законом Ньютона (кстати, закон Ньютона, как пишут в старых энциклопедиях, был на латыни и без обозначений). Всё объяснялось механикой. Всё простое и объяснимое, в конце концов, побеждает. Так было и с открытием Коперника. Но не тут-то было. На этот раз руководство масонской ложи во время углядело опасность в таком открытии. Это не входило в планы масонов. Труды Фатио остались не напечатанными.

Спустя более полувека в 1748 или в 1756 году бумаги с работой Фатио находит другой швейцарский учёный тоже уроженец Женевы Ле Саж. Но ситуация не изменилась. Данная теория находилась под негласным, как и всё связанное с масонской ложей, запретом. Ле Саж также не смог опубликовать эту теорию. Когда умудрились опубликовать о том, что такая теория существовала, разобраться теперь трудно. Одни уверяют, что в начале 20 века, другие, что в конце 19 века. Вероятно, в конце 19 века, так как пишут, что сам Максвелл опровергал эту теорию. Точно нам уже об этом не узнать.

Скрыть о том, что такая теория была и что её не печатали, трудно и поэтому об этом упоминают, но под своим соусом. Вот об этом в ВИКИПЕДИИ

http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E8%FF_%E3%F0%E0%E2%E8%F2%E0%F6%E8%E8_%CB%E5%F1%E0%E6%E0

 

Используемые источники

1. Николаев С.А. “Эволюционный круговорот материи во Вселенной”. 6-ое издание,

СПб, 2010 г., 320 с.

2. Николаев С.А. ”Ошибочный перевод Эйлера законов Ньютона“. СПб, 2011 г., 44 с.

3. Николаев С.А. “Постоянна ли скорость света? Конечно, нет”, СПб, 2012 г., 40 с.

4. Энциклопедии.